엑셀에서 표준편차를 계산하는 방법(표준 편차 이해 및 계산하는 절차 설명)

통계 자료를 분석할 때 표준 편차를 이용하여 데이터를 분석하는 경우가 많습니다.

이번 글에서는 엑셀에서 표준편차를 계산하는 방법(표준 편차 이해 및 계산하는 절차 설명)에 대해 알아보겠습니다.

표준편차(Standard Deviation)란 무엇인가?

표준 편차를 영어로 Standard Deviation이라고 합니다.

‘표준(Standard)‘는 평균적이라는 의미이고, ‘편차(Deviation)‘은 벗어난 정도를 의미합니다.

간단히 설명해서 표준편차란 데이터가 평균에서 얼마나 떨어져 있는지 확인하기 위한 측정 값을 말합니다.
즉, 데이터의 변동성을 해석하는 데 사용되는 중요한 통계적 측정 값이라고 할 수 있습니다.

표준 편차가 낮을수록 데이터가 평균에 더 가깝다는 것을 의미하고, 표준 편차가 높을수록 데이터가 평균에서 더 멀리 떨어져 있음을 보여줍니다.

따라서 표준 편차만 봐도 데이터 값 집합의 분산 정도를 확인할 수 있습니다.

표준편차 계산 방법

표준편차를 계산하기 위해 몇 단계의 계산 과정을 거칩니다.

▼ 아래 화면 이미지의 각 STEP에 대한 설명을 잘 보시기 바랍니다.

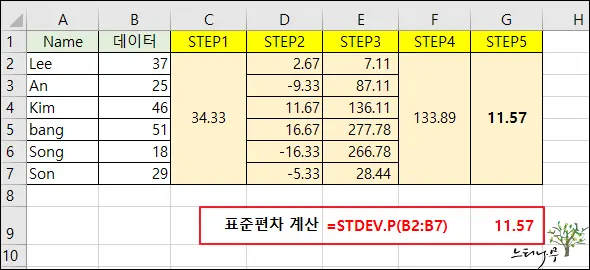
STEP 1. 데이터 집합의 평균을 계산합니다.

• 데이터 집합의 모든 값을 더한 다음 그 합계를 집합의 총 개수로 나누어 데이터 집합의 평균을 계산합니다.
• =SUM(B2:B7)/COUNT(B2:B7)
• (37+25+46+51+18+29)/6 → 34.33

STEP 2. 각 데이터에서 평균을 뺍니다.

• 데이터 집합의 각 데이터에서 평균 값을 뺍니다.
• =B2-$C$2
• 37-34.33 → 2.67

STEP 3. 두 번째 단계(STEP2)에서 계산한 값에 제곱 합니다.

• 2단계에서 계산한 차이 값을 제곱 합니다.
• =D2^2
• 2.67^2 → 7.11

STEP 4. 세 번째 단계(STEP3)에서 계산한 제곱 값의 평균을 계산합니다.

• 3단계에서 계산한 차이 제곱의 평균을 계산합니다.
• =SUM(E2:E7)/COUNT(E2:E7)
• (7.11+87.11+136.11+277.78+266.78+28.44)/6 → 133.89

STEP 5. 네 번째 단계(STEP4)의 평균 제곱 값의 제곱근을 계산합니다.

• 표준 편차를 구하는 마지막 단계로 제곱 평균의 제곱근을 계산해서 표준 편차를 구합니다.
• =SQRT(F2)
• 133.89의 제곱근 → 11.57

엑셀 SQRT 함수를 사용하여 표준편차 구하기

앞 단락에서 표준 편차가 계산되는 과정에 대해 알아보았습니다.
표준 편차에 대한 개념 및 계산 과정을 이해했다면 이제 엑셀에서 간단하게 함수를 사용하여 쉽게 표준편차를 구하는 방법에 대해 알아보겠습니다.

1. 엑셀에서 표준 편차를 구하는 함수는 STDEV.P 입니다.

2. 기본 Syntax는 다음과 같습니다.

• STDEV.P(number1, [number2], …)
• 설명 : 모집단의 표준 편차를 구합니다. 텍스트와 논리값은 제외됩니다.
• number1, … : 인수는 모집단에 해당하는 인수로서 255개까지 지정할 수 있습니다.

3. 앞 단락에서 5단계로 계산 한 표준 편차를 아래와 같이 하나의 수식으로 처리할 수 있습니다.

• =STDEV.P(D2:D7)
• 결과 값은 앞 단락에서 단계 별로 계산 한 표준 편차 값과 동일하게 계산됩니다.

마무리

이상으로 표준 편차에 대한 개념과 계산 절차 그리고 엑셀 함수를 이용한 표준 편차 계산에 대해 알아보았습니다.

참고로 각 계산 단계에서 계산 결과는 보기 편하도록 소수점 2자리까지 표시되도록 하였습니다.

더 큰 모집단에서 표본의 표준 편차를 추정하는 표본 집단의 표준 편차를 구하는 STDEV.S 함수도 참고해 보세요.
STDEV.P 함수와 사용 방법은 동일합니다.

♥ 이 글이 도움이 되었기를 바랍니다. ^-^
댓글로 흔적을 남겨 주세요.